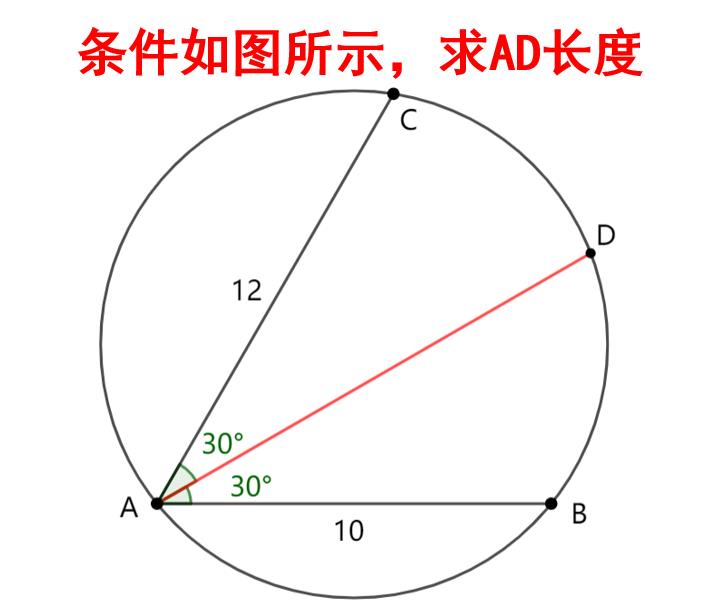
题目：

条件如图所示，求AD长度

知识点回顾：

余弦定理

对于任意三角形，任何一边的平方等于其他两边平方的和减去这两边与它们夹角的余弦的积的两倍。

正弦定理

一个三角形中，各边和所对角的正弦之比相等，且该比值等于该三角形外接圆的直径（半径的2倍）长度

阿基米德折弦定理

阿基米德折弦定理：一个圆中一条由两根长度不同的弦组成的折弦所对的两段弧的中点在较长弦上的射影，就是折弦的中点。AB和BC组成圆的折弦，AB>BC，M是弧ABC的中点，MF⊥AB，垂点为F。则AF=BF+BC。

粉丝解法1：

由余弦定理可得，BC^2=12^2+10^2—2×12×10cos60°=124→BC=2√31。由正弦定理可得圆的半径：r=BC÷（2sin60°）=2√93/3，因BD=DC=r所以由折弦定理可得：AD^2=AB×AC+BD^2 =1452/9，故有：
AD=22√3/3。

粉丝解法2：

粉丝解法3：

粉丝解法4：

口算

粉丝解法5：

如图：BD＝CD，记AD＝a，据余弦定理有12＾2＋a＾2－2x12xaxcos30＝10＾2＋a＾2－2x10xaxcos30，a＝22√3/3。

粉丝解法6：

粉丝解法7：

粉丝解法8：

过B点做直线垂直AD，交AD于点E，延长交AC和圆于点G和F；连接FC， △ABG和△GCF均为等边三角形；AE=5√3 ;GF=2; EF=7;

圆周角∠BFD=∠BAD=30°，ED=7√3/3

AD=AE+ED=22√3/3